♟️ Why game theory matters in machine learning

Game theory is an interdisciplinary research field that studies games and strategies in games. A concept in Game Theory is what's called "Nash Equilibrium". In a game, you want to reach this equilibrium at each move.
This means that no improvement can be made and that no change will increase your dividend or success, given that the other player continues to play as excepted.

Now, a team consisting of Ian Gemp, Thore Graepel, Brian McWilliams, and Claire Vernade at the AI-company DeepMind, owned by Google, has published an article entitled "EigenGame: PCA as a Nash Equilibrium." The article shows how the concept of Nash Equilibrium can be useful in data analysis and machine learning.

What is PCA?

A very common method used to analyze data is what is called "PCA." PCA is about creating meaning in data by understanding which "recipe" best describes how the data is spread in a coordinate system. And through the recipe, understand which dimension of the data most contributes to a certain spread.

The data may, for example, be individuals of trees whose height, radius, age, and number of branches have been measured. To find the best recipe, a computer needs to perform a lot of calculations. But researchers believe it is possible to optimize PCA further. A recipe is called the "principal component."

In the research article from DeepMind, the researchers reinterpret PCA as a game. We asked the researchers behind the article how their game "Eigengame" works.

"EigenGame views each of the principal components of principal component analysis (PCA) as a player in a game. At the Nash equilibrium of EigenGame, each player is in a stalemate with the rest, at which point the optimal principal components have been found"

Ian Gemp, a researcher at DeepMind, explains with an analogy.

"You can imagine EigenGame in three dimensions. Imagine three players being randomly released in three places on the globe, and there are three prizes in three other places. The game is about finding the prizes, but the players will be penalized if they move towards the same prize. In more dimensions you add players, prizes and they play on a sphere with more dimensions."

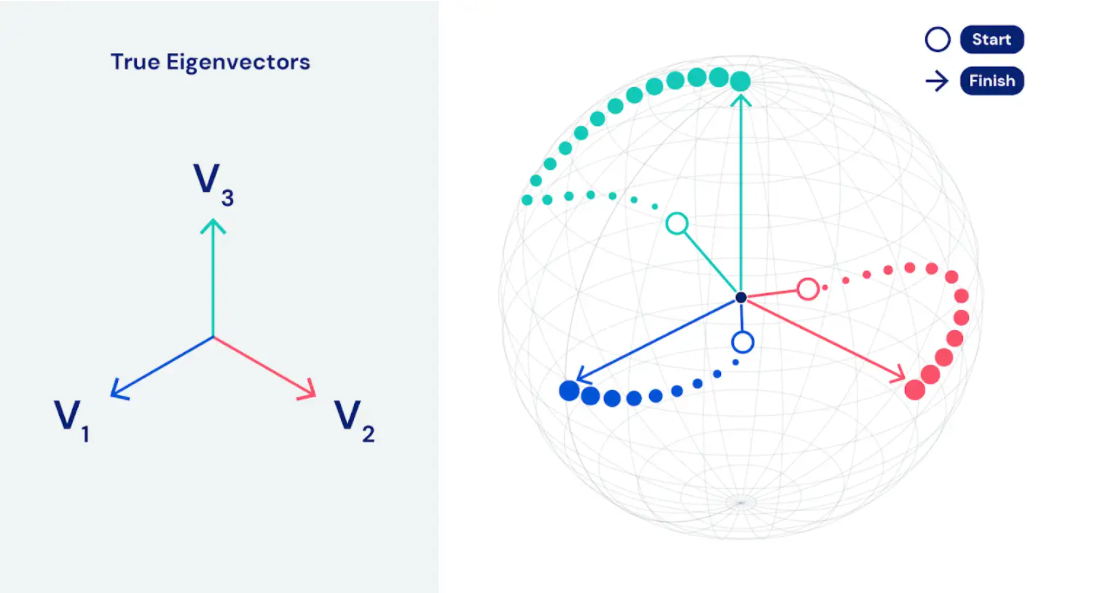
Eigengame has been used to analyze a large language database of about 100 TB but could also be used in genetic research and can analyze up to tens of millions of genetic variations.

Will you apply the logic of Game Theory to other problems?

"Absolutely. We already are in the process of applying this same line of thinking to other fundamental math problems that support a wider range of data analysis tools."

Read the full paper here.